3D Gaussian Splatting 解读
Siggraph 2023 Best Paper!
强烈去看 b 站 up 主中恩实验室的系列视频!
1. 引言
1.1 任务
文章涉及到的任务是三维重建+渲染。
文章提出了一种新方法实现了辐射场的实时渲染,能够在较少的训练时间中,实现SOTA级别的视觉效果,针对用多张照片和视频拍摄的场景,允许以 1080p 分辨率进行高质量的实时(≥ 30 fps)新视图合成。
可以先用一句话表达 3D Gaussian Splatting 干了什么:使用 3D Gaussian 球表示三维模型,并通过 Splatting 技术渲染出来。
事实上,用椭球集来表示三维模型不是一个很新鲜的事儿,早在 1994 年的游戏《魔城迷踪ecstatica》中,就出现了:

1.2 对比
对比 Nerf 和传统的 Mesh:一个是纯连续的、隐式表达在可微空间内;一个是纯离散的(虽然可以插值)、显式表达在三维空间内,3DGS 是在离散和连续间的一个平衡:在高斯球内部是连续的、可微的;在整个空间中,每个高斯球又是离散的。所谓中庸之道也。
1.3 可视化
我们可以使用论文作者们提供的可视化工具来直观地看看如何使用椭球表示三维模型:


可以看到,随着 scale 的增加,一个个椭球体从原来的圆点逐渐变化成更“高级”的椭球体,而这些变化之后的椭球体,就组成了整个模型。如果你觉得这很酷,请接着往下看。
2. 动机
传统的 3D 模型表示方法,如 离散的Mesh 和点云,以及连续的 Nerf,通常面临着一个主要问题:随机采样过程中产生的噪声,这直接影响了渲染质量。此外,这些方法在渲染速度和渲染质量之间不可兼得。
为了解决这一问题,论文提出了3D Gaussian Splatting(3DGS)。这种技术通过结合离散和连续表示方法的优势,不仅克服了传统方法在噪声和渲染质量方面的限制,而且极大地提高了渲染速度。
3. 贡献
- 引入3D gaussian作为 3D 表示,高效,准确,无结构 。
- 3D gaussian的优化算法:Clone 和 剪枝。
- 快速可微渲染器。
4. 方法
在介绍具体的实现方法之前,我们先来拆解一下论文的标题《3D Gaussian Splatting for Real-Time Radiance Field Rendering》:
3D Gaussian: 是文章构建模型的核心元素,即三维高斯球。
Splatting:是一种传统的 3D -> 2D 的光栅化渲染方式 。不过,文章中的 Splatting 方法和传统的有所区别,之后会讲到。
Radiance Field: 即辐射场。辐射场(RF)是用于表达三维空间中光的分布和光强的一个模型(你也可以认为是一种光场)。另外,之前一直大火的 NeRF 模型,就是一种面向这种场,在三维隐式空间中建模的深度学习模型。在基于 Nerf 的表示方法下,三维空间被表示为一组可学习且连续的辐射场,输入视角+位置学习后,可以得到密度+色彩。从数学上来说,辐射场可以被描述为一个函数 L ,将空间中的一个点 $(x,y,z)$ 和一个由球坐标 $(θ,ϕ)$ 指定的方向映射到一个非负的辐射值。
3D 高斯表示的辐射场公式如下:
$$
L_{3DGS}(x, y, z, \theta, \phi) = \sum_i G(x, y, z, \mu_i, \Sigma_i) \cdot c_i(\theta, \phi),
$$(由于我是物理专业的,这勾起了一些我关于光学的痛苦记忆…)**Real-Time Rendering: 实时渲染,即从三维重建后的模型,渲染到二维的显示。这是非常重要的一步。实时是指这种方法的速度非常快,可以达到实时级别(>30 FPS)。
那么,接下来,我们就以这几部分为基础进行展开,依次进行介绍。
4.1 3D Gaussian
数学细节请参考之后的 附录。
4.1.1 引入
就像给 3 个顶点能表达任意一个 3D 三角形,继而很好的构建三维模型( Mesh 的思想),研究者自然希望构建三维模型的基础元素能覆盖足够多样的几何体,而椭球就是一种很好的基础元素。
但是,只使用一个个实椭球来构建模型,就会像引言中的魔城迷踪游戏一样,远远不够。这时,我们就想寻找一种方式,来将椭球这种元素变得“强大”一点——能够构建出多样的表示。
那么,如果将椭球的边界变得不清晰,成为一个渐变的,可以融合的呢?如同真实世界中的“黑滴效应”:当你将两个物体慢慢相互靠近直到重叠时,这两个物体的影子之间的颜色会慢慢变深,形成黑滴状:

我们可以看到,如果这样的话,椭球就不再是那个有清晰边界的椭球了。继而,我们可以构建出更多样的表达。由此,我们便会想到概率分布,再由椭球的形状,我们又会想到同样是椭球状的三维高斯分布。
4.1.2 构建
既然我们想到可以用三维高斯分布来构建基础元素,那么这个元素有什么属性,如何构建生成新的椭球呢?
论文中,三维高斯体的属性有其中心(位置)$\mu$、不透明度 $\alpha$、三维协方差矩阵(表示缩放程度)$\Sigma$ 和颜色 $c$ 。$c$ 用球谐函数表示(具体请参考 附录),以呈现视角依赖的外观。所有属性都是可学习的,并通过反向传播进行优化。
论文给出了初始化方法是使用放缩变换 $S$ 和旋转变换 $R$ 组合得到 $\Sigma$:
$$
\Sigma = RS{S}^T{R}^T
$$
由于放缩变换都是沿着坐标轴,所以只需要一个3D向量 $s$,旋转则用四元数 $q$ 表达。机器学习通常使用梯度下降对参数进行优化,但直接优化 $\Sigma$ 难以保证半正定,所以论文的方法是继续将梯度传递到 $s,q$ 进行优化。
至于如何自适应地生成新椭球,请参阅 密度控制 一节。
4.2 Splatting
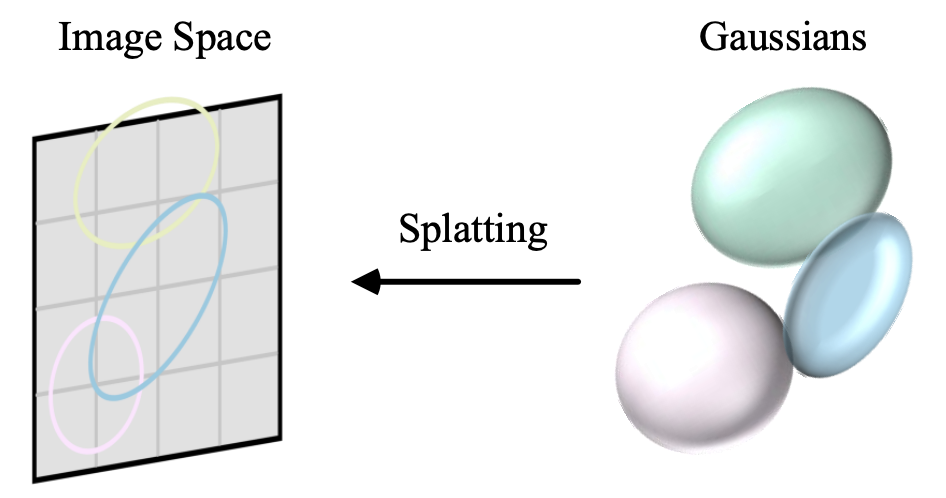
在这一步中,三维高斯椭球体被投影到二维图像空间椭圆形,以进行渲染。
Splatting 的中文翻译为:抛雪球法。很形象,我们可以想象一下,把一个雪球(高斯球)扔到一个玻璃盘子上,雪球散开以后,在撞击中心的雪量(对图像的贡献)最大,而随着离撞击中心距离的增加,雪量(贡献) 减少。脑补一下盘子上的图像,其实我们可以自然而然的想到二维高斯分布的密度函数。
对比示意图如下,抛雪球的图由 ChatGPT4 使用 DALL-E 绘制:

而这个把椭球投影到平面后得到的 2D 图形,就是 Splatting 渲染方法,如下图(摘自A Survey on 3D Gaussian Splatting)
4.2.1 原理
数学上来说,给定视图变换 W 和三维协方差矩阵 $\Sigma$ ,计算投影的二维协方差矩阵 $\Sigma ‘$ 使用以下公式:
$$
\Sigma’ = J W \Sigma W^T J^T
$$
其中 $J$ 是射影变换的仿射近似的雅可比矩阵。(细节请参考附录中的投影变换一节)
4.2.2 渲染
论文的渲染方法为 Tiled-based Rasterizer,其流程为:
预处理:在这一步骤中,3D 高斯的参数(协方差、位置、不透明度、球谐函数)被优化,以适应给定的图像序列和视角。这一步骤可以使用梯度下降或其他优化算法来实现,目标是最小化重建误差。此外,还可以使用自适应密度控制(ADC)来调整 3D 高斯的数量和分布,以达到最佳的渲染效果。
投影:在这一步骤中,3D 高斯(椭球)被投影到 2D 图像空间(椭圆)中进行渲染,如图 2a 所示。给定视图变换${W}$和 3D 协方差矩阵${\Sigma}$,投影的 2D 协方差矩阵${\Sigma}’$可以使用以下公式计算:
$$
{\Sigma}’ = {JW \Sigma W}^T {J}^T
$$其中${J}$是一个将 3D 向量转换为 2D 向量的矩阵。投影的 2D 高斯的中心位置和颜色可以直接从 3D 高斯的参数中得到。投影的 2D 高斯的不透明度需要根据 3D 高斯的不透明度和协方差矩阵进行调整。具体来说,投影的 2D 高斯的不透明度$\alpha’$可以使用以下公式计算:
$$
\alpha’ = 1 - \exp \left( -\frac{\alpha}{\sqrt{\det ({\Sigma})}} \right)
$$排序:在这一步骤中,投影的 2D 高斯被按照其深度值进行排序,以便在后续的渲染过程中正确地处理遮挡关系。为了提高排序的效率,可以使用空间划分或其他加速技术来减少排序的复杂度。例如,可以将图像平面划分为多个块,然后对每个块内的 2D 高斯进行排序,如图 2b 所示。
渲染:在这一步骤中,投影的 2D 高斯被用于生成最终的合成图像。
4.2.2.1 分块
在处理图像时,为了减少对每个像素进行高斯运算的计算成本,论文采用了一种不同的方法:它不是在像素级别进行精确计算,而是将精度降低到了更宏观的图块级别。这个过程首先涉及将整个图像划分成多个不重叠的小块,这些在原始的研究论文中被形象地称为“砖块”。按照原始论文的建议,每个砖块包括 16 $\times$ 16 个像素。
接下来,会进一步识别出哪些砖块与特定的高斯投影相交。考虑到一个高斯投影可能会覆盖多个砖块,一种有效的处理方式是复制这个东西,并为每个复制出的高斯分配一个唯一的标识符,即与之相交的 Tile 的 ID。这样,每个砖块都与一个或多个高斯相关联,这些高斯标识了该砖块在图像中的位置和重要性。通过这种方式,3DGS 能有效地降低计算复杂度,同时还保持了图像处理的效率和准确性。
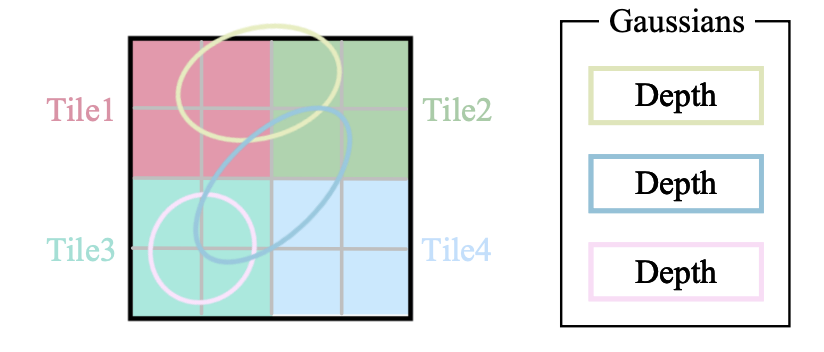
另外,论文的官方实现代码使用了多种加速方式,如并行渲染。具体请去看官方仓库。
4.2.2.2 排序 & Alpha Blending
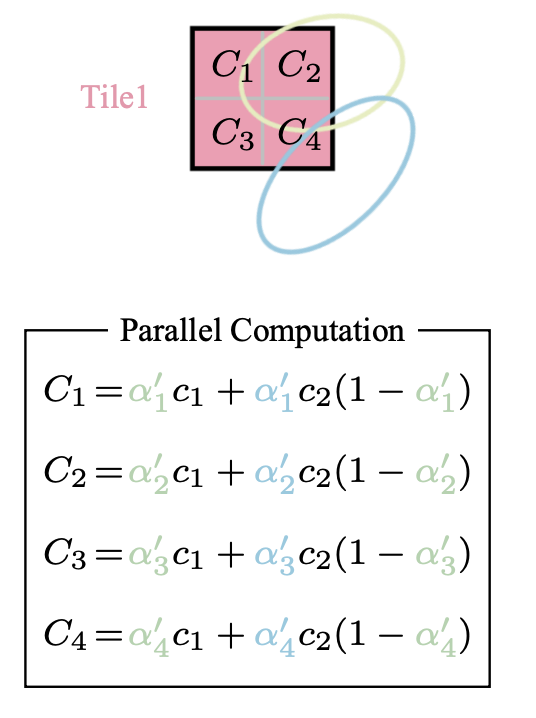
给定像素位置 $x$,通过视图变换 $W$,可以计算与所有重叠高斯体的距离,即这些高斯体的深度,形成高斯体的排序列表 $N$。然后,进行Alpha Blending,也就是混合 alpha 合成来计算整体图像的最终颜色:
$$
C = \sum_{i \in N} c_i \alpha_i’ \prod_{j=1}^{i-1} (1 - \alpha_j’) ,
$$
其中 $c_i$ 是学到的颜色,最终的不透明度 $\alpha_i’$ 是学到的不透明度 $\alpha_i $ 与高亮的亮度:
$$
\alpha_i’ = \alpha_i \times \exp \left( -\frac{1}{2} (x’ - \mu_i’)^T \Sigma_i’^{-1} (x’ - \mu_i’) \right) ,
$$
其中 $x’$ 和 $\mu_i’$ 是投影到同一的坐标系。
另外,如果不透明度为 1 的话,每个椭球体就是有着清晰边界的椭球了,就像这样:

4.3.3.3 由 3D 到 2D
3D Gaussian -> 2D Gaussian的过程是非常重要的。
论文中引用的核心文章《EWA volume splatting》描述了如何将3D高斯通过仿射变换转换为新的3D高斯分布,并与画布像素对齐。这一变换后,通过沿第三维积分,可以计算出椭球在特定像素上的着色。由于3D高斯分布沿任一轴线积分的结果是2D高斯,因此可以用2D高斯来简化积分过程。
和这篇笔记的作者一样,我认为这个过程是 3D Gaussian Splatting 的一个关键创新点。传统的基于体积和积分的渲染方法需要选择采样点来查询隐式几何形状,并将其属性变换累加以计算像素颜色。这不仅要保证渲染质量和隐式几何的连续性,还要维持细节的还原度,且不可避免地存在误差。因此,通常需要增加采样量,这会导致性能下降。3D高斯的轴向积分与2D高斯等价,从数学角度解决了对大量采样的需求,将计算量限制在高斯数量上,这实在是非常的 Cooool!
另外,这些高斯可以通过光栅化管线进行快速并行渲染,进一步提高效率。
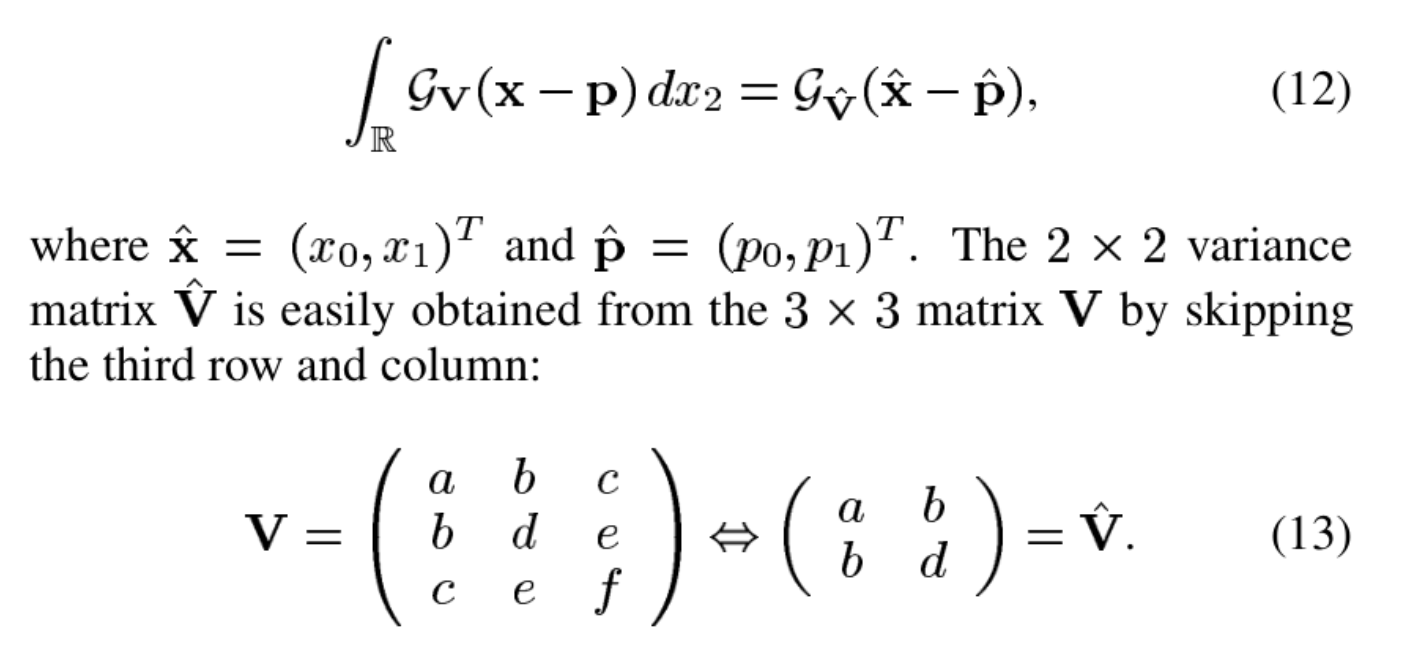
从相机空间到光线空间是一个非仿射变换,这意味着不可能使用单一的线性变换矩阵来转换所有点的坐标。这是因为每个点在光线空间的坐标是一个以其在相机空间坐标为自变量的非线性函数,所以不存在一个通用的变换矩阵。
所以作者使用了一个近似方法。这个方法使用每个三维高斯的中心点坐标经过的变换矩阵来近似整个高斯的变换矩阵。通过这种方式,每个高斯的变换可以被视为一个仿射变换。这种特定的变换矩阵被称为雅可比矩阵$(J)$:
$$
J = \begin{pmatrix}
\frac{1}{u_2} & 0 & -\frac{u_0}{u_2^2} \
0 & \frac{1}{u_2} & -\frac{u_1}{u_2^2} \
\frac{u_0}{l’} & \frac{u_1}{l’} & \frac{u_2}{l’}
\end{pmatrix}
$$
最后,对于每个给定的三维高斯的协方差矩阵$V’’$,以及其 world space 下的中心点坐标$(u0,u1,u2)$,我们可以求得 ray space 下的高斯协方差。由于给的是 world space 下的坐标,所以得先乘以旋转平移矩阵 $W$ 转化为相机空间坐标,然后通过中心点坐标求出雅可比矩阵 $J$,光线空间下的高斯协方差就如下:
$$
V = JWV’’W^TJ^T = T^3D_V’’T^3D^T_SD^N
$$
在正投影下,三维高斯协方差矩阵的前两行和两列直接构成了投影到图像平面的二维高斯协方差矩阵。二维高斯的中心点坐标是通过将相机空间中的 $ u_0 $ 和 $u_1$ 坐标除以第三维坐标 $u_2$ 来获得,即中心点坐标为 ($u_0/u_2, u_1/u_2$) 。
通过这种方法,我们就可以把三维空间中的高斯分布转换成图像平面上的二维高斯分布。
5. 总体的 pipeline
5.1 总体流程
论文中的总流程图:
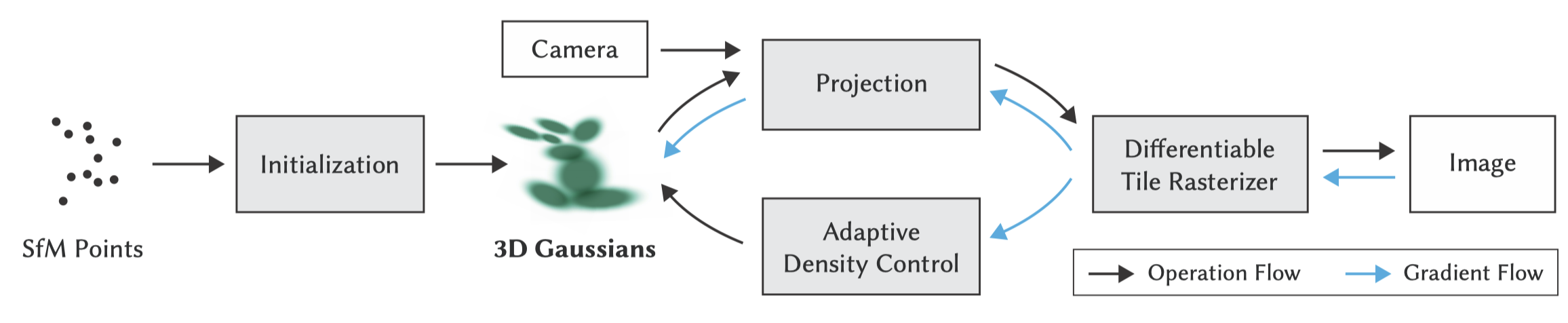
系统首先对 SfM 点云进行了初始化,得到 3D 高斯球们,然后借助相机外参将点投影到图像平面上(即Splatting),接着用可微光栅化,渲染得到图像。得到渲染图像Image后,将其与Ground Truth图像比较求loss,并沿蓝色箭头反向传播。蓝色箭头向上,更新3D高斯中的参数,向下送入自适应密度控制中,更新点云。
5.2 SfM
SfM (Structure from Motion,运动恢复结构) 是一种从一组图像中估计出点云的方法。
SfM 初始化点云过程的主要步骤如下:
- 对每一张图像,使用 SIFT、SURF、ORB 等算法提取特征点,并计算特征描述子。
- 对相邻的图像,使用 KNN、FLANN 等算法进行特征匹配,筛选出满足一致性和稳定性的匹配对。
- 对匹配的特征点,使用 RANSAC、LMedS 等算法进行异常值剔除,提高匹配的准确性。
- 对匹配的特征点,使用多视图几何的约束,如基础矩阵、本质矩阵、单应矩阵等,进行相机位姿的估计,以及三维坐标点的三角化。
- 对估计的相机位姿和三维坐标点,使用 BA(Bundle Adjustment)等算法进行优化,以减少重投影误差和累积误差。
初始点的示例:

5.3 自适应密度控制
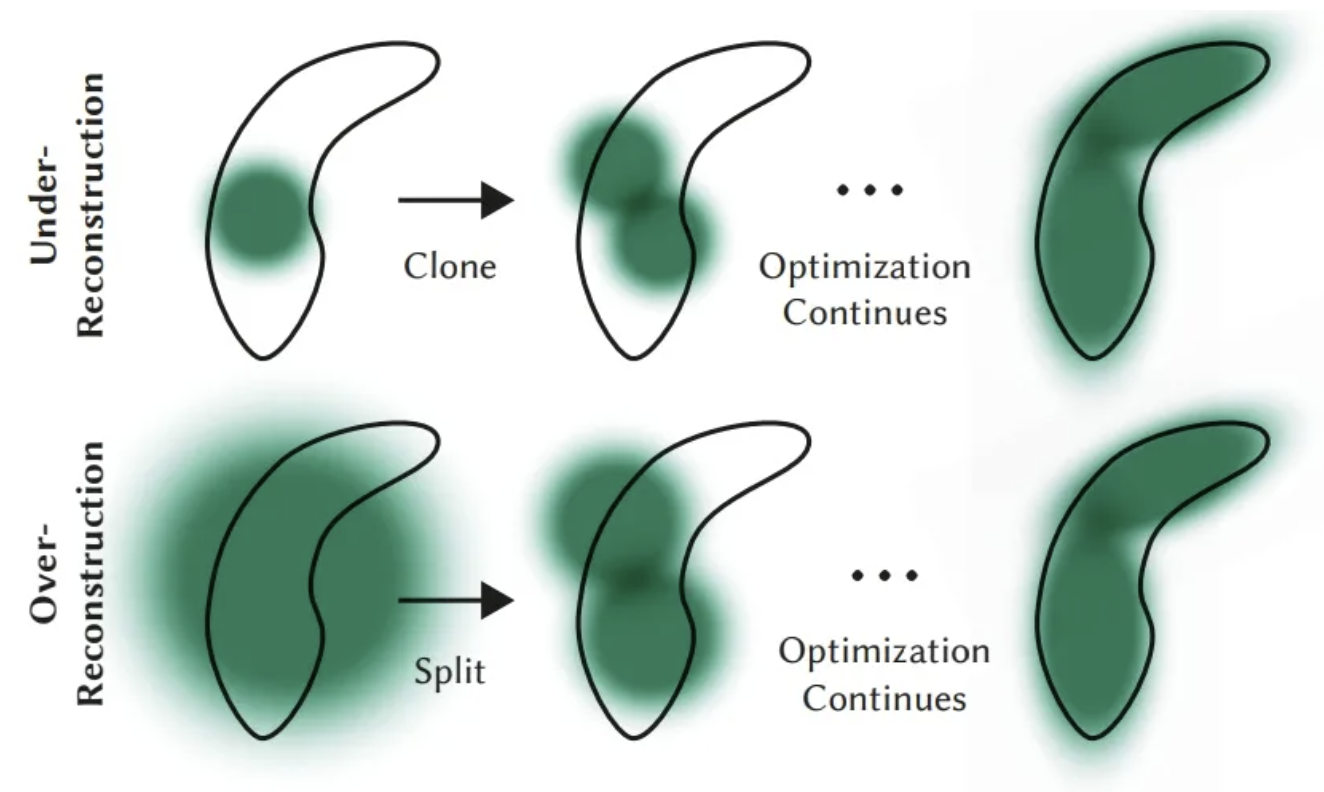
初始化:3DGS建议从SfM产生的稀疏点云初始化或随机初始化高斯,可以直接调用 COLMAP 库来完成这一步,然后进行点的密集化和剪枝以控制3D高斯的密度。当由于某种原因无法获得点云时,可以使用随机初始化来代替,但可能会降低最终的重建质量。
点密集化:在点密集化阶段,3DGS自适应地增加高斯的密度,以更好地捕捉场景的细节。该过程特别关注缺失几何特征或高斯过于分散的区域。密集化在一定数量的迭代后执行,比如100个迭代,针对在视图空间中具有较大位置梯度(即超过特定阈值)的高斯。其包括在未充分重建的区域克隆小高斯或在过度重建的区域分裂大高斯。对于克隆,创建高斯的复制体并朝着位置梯度移动。对于分裂,用两个较小的高斯替换一个大高斯,按照特定因子减小它们的尺度。这一步旨在于 3D 空间中寻求高斯的最佳分布和表示,增强重建的整体质量。
点的剪枝:点的剪枝阶段移除冗余或影响较小的高斯,可以在某种程度上看作是一种正则化过程。一般消除几乎是透明的高斯(α低于指定阈值)和在世界空间或视图空间中过大的高斯。此外,为防止输入相机附近的高斯密度不合理地增加,这些高斯会在固定次数的迭代后将$\alpha$设置为接近0的值。该步骤在保证高斯的精度和有效性的情况下,能节约计算资源。
5.4 优化
这部分,原始论文的伪代码已经足够清晰,我把它翻译成中文,各位细品一下。

6. 限制
优点
- 高品质、逼真的场景
- 快速、实时的渲染
- 更快的训练速度
缺点
- 防止模型优化中的“破碎”的高斯:点太大、太长、冗余等
- 更高的显存使用率 (4GB 用于显示,12GB 用于训练)
- 更大的磁盘占用 (每场景 1GB+)
- 与现有渲染管线不兼容
7. 应用
同时定位与地图构建(SLAM)
SLAM是机器人学和自动系统的核心计算问题。它涉及机器人或设备在未知环境中理解其位置的同时,映射环境布局的挑战。SLAM在各种应用中至关重要,包括自动驾驶车辆、增强现实和机器人导航。SLAM的核心是创建一个未知环境的地图,并实时确定设备在此地图上的位置。因此,SLAM为计算密集型场景表示技术提出了巨大挑战,同时也是3D GS的良好测试平台。
动态场景建模
动态场景建模指的是捕捉和表示随时间变化的三维结构和场景外观的过程。这涉及创建一个数字模型,准确反映场景中对象的几何形状、运动和视觉方面的变化。动态场景建模在虚拟现实、增强现实、3D动画和计算机视觉等多个应用领域至关重要。4D 高斯散射(4D GS)将3D GS的概念扩展到动态场景。它包含了时间维度,允许表示和渲染随时间变化的场景。
人工智能生成内容(AIGC)
AIGC 指的是由人工智能系统自主创造或显著改变的数字内容,特别是在计算机视觉、自然语言处理和机器学习领域。AIGC的特点是它能模拟、扩展或增强人类生成的内容,使其应用范围从逼真的图像合成到动态叙事创作。AIGC的重要性在于其跨越娱乐、教育和技术发展等各个行业的变革潜力。它是数字内容创造不断演变景观中的关键要素,提供了与传统方法相比更具可扩展性、可定制性和通常更高效的替代方案。
附录
0. 术语解释
场景重建与渲染
场景重建:从一组图像集合或其它数据建立场景的三维模型。
渲染:将计算机可读取的信息(如场景中的3D物体)转化为图像。 早期技术基于光场生成逼真的图像,运动结构(SfM)与多视图立体匹配(MVS)算法通过从图像序列估计3D结构来增强光场。
神经渲染和辐射场
神经渲染:将深度学习与传统图形技术结合生成逼真的图像。早期方法使用CNN估计混合权重或纹理空间解决方案。
辐射场:一种函数表达,描述从各方向穿过空间各点的光的量。NeRF使用神经网络建模辐射场。
体积表示和光线行进
体积表达:不仅将物体和场景建模为表面,还将其其建模为充满材料或空白空间的体积。这样可以对如雾、烟或半透明材料进行更精确的渲染。
光线行进:是体积表达渲染图像的技术,通过增量跟踪穿过“体”的光线来渲染图像。NeRF引入重要性采样和位置编码增强合成图像的质量,虽然能得到高质量的图像,但这一方法计算量大。
基于点的渲染
基于点的渲染是一种使用点而非传统多边形来可视化3D场景的技术。该方法特别适用于渲染复杂、非结构化或稀疏的几何数据。点可以通过添加额外属性,如可学习的神经描述符来进行增强,并且可以高效地进行渲染,但这种方法可能会出现渲染中的空洞或混叠效应等问题。3DGS通过使用各向异性高斯进行更连贯的场景表达。
1. 背景知识
1.1 三维高斯分布
在三维空间中,一个高斯分布可以用其均值向量 ($\boldsymbol{\mu}$) 和协方差矩阵 ($\boldsymbol{\Sigma}$) 来描述。均值向量定义了分布的中心位置,而协方差矩阵则描述了分布在不同方向上的扩散情况。
1.1.1 均值和协方差
均值向量 ($\boldsymbol{\mu}$): 它是一个三维向量 ($\boldsymbol{\mu} = [\mu_x, \mu_y, \mu_z]^T$),表示分布在x、y、z轴上的平均位置。
协方差矩阵 ($\boldsymbol{\Sigma}$): 它是一个3x3的对称矩阵,表示如下:
$$
\boldsymbol{\Sigma} = \begin{bmatrix} \sigma_{xx} & \sigma_{xy} & \sigma_{xz} \ \sigma_{yx} & \sigma_{yy} & \sigma_{yz} \ \sigma_{zx} & \sigma_{zy} & \sigma_{zz} \end{bmatrix}
$$
其中,$(\sigma_{xx}), (\sigma_{yy}), (\sigma_{zz}) $分别是x、y、z轴上的方差,而其他元素比如$ (\sigma_{xy}) $是 x 和 y 之间的协方差。
1.1.2 方差与协方差的关系
- 方差是描述单个随机变量波动程度的量度,而协方差是描述两个随机变量如何一起变化的量度。
- 在协方差矩阵中,对角线元素(方差)描述了各个轴上的分布宽度,而非对角线元素(协方差)描述了不同轴之间的相关性。
1.1.3 概率密度函数
三维高斯分布的概率密度函数(PDF)为:
$$
f(\mathbf{x} | \boldsymbol{\mu}, \boldsymbol{\Sigma}) = \frac{1}{\sqrt{(2\pi)^3 |\boldsymbol{\Sigma}|}} \exp\left(-\frac{1}{2}(\mathbf{x} - \boldsymbol{\mu})^T \boldsymbol{\Sigma}^{-1} (\mathbf{x} - \boldsymbol{\mu})\right)
$$
其中 $\mathbf{x}$ 是一个三维点,$\boldsymbol{\Sigma}$ 是协方差矩阵,|$\boldsymbol{\Sigma}$| 是协方差矩阵的行列式,$\mu$ 是均值。
之后,进行标准化,默认模型坐标中心在原点,方便旋转放缩,放入世界空间时再加上平移,我们就得到了论文中的定义的三维高斯分布公式(5):
$$
G(x) = e^{-\frac{1}{2} x^T \Sigma^{-1} (x)}
$$
此外,你可以自行对比一下一维的高斯分布 PDF:
$$
f(x|\mu, \sigma) = \frac{1}{\sigma \sqrt{2\pi}} \exp\left(-\frac{(x - \mu)^2}{2\sigma^2}\right)
$$
1.1.4 方差对旋转和缩放的影响
- 缩放:方差值越大,表示在该轴上分布越分散。也就是说,点在该方向上的分布范围更广。
- 旋转:协方差矩阵的非对角线元素(协方差)如果不为零,则表示两个轴之间存在相关性。这种相关性使得分布呈现出一定的倾斜或旋转,而这种倾斜正是由于两个轴之间的线性关系造成的。
通过调整协方差矩阵,可以改变高斯分布在空间中的形状和方向,演示如下:
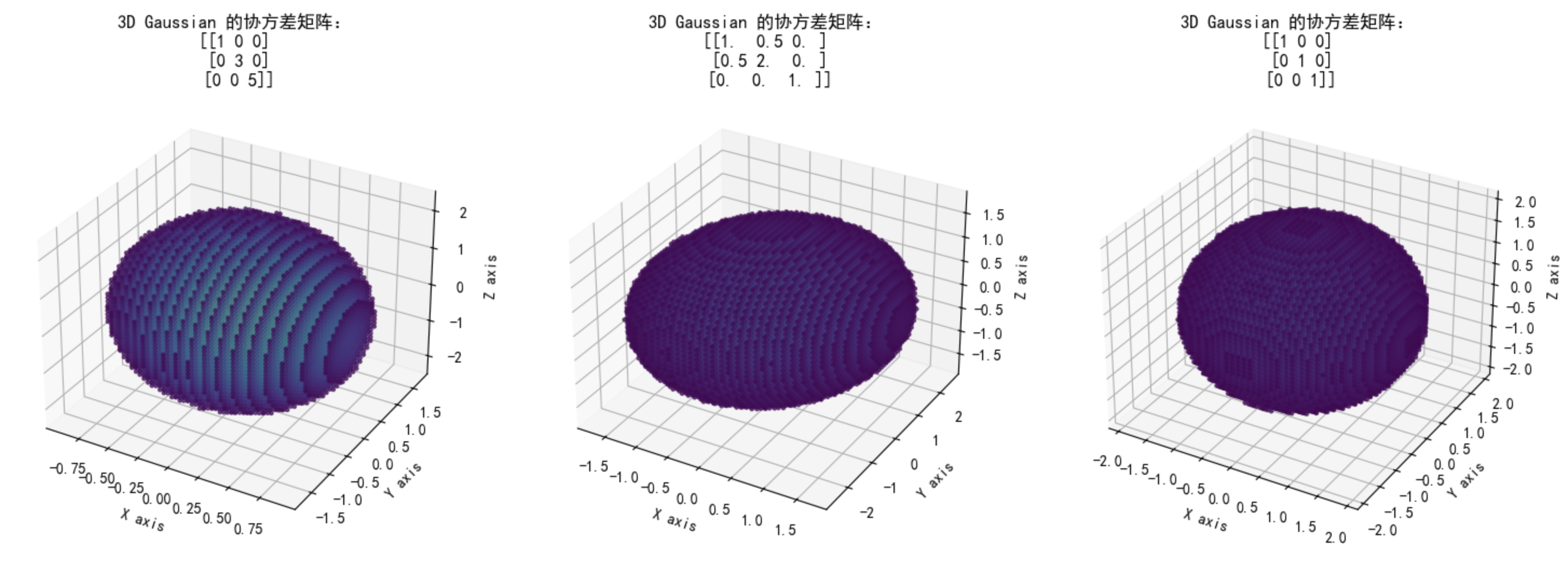
(注:为了演示清楚这个椭球形状,我去掉了值小于 0.01 的点)
第一个子图(左):这个高斯分布沿着z轴具有大的方差,因此在z轴方向上更加扁平和分散。由于没有协方差,椭球保持着正向的姿态。
第二个子图(中):这里的高斯分布在 x 和 y 轴之间有大的协方差。这种协方差导致椭球沿x和y轴倾斜。
第三个子图(右):方差在所有轴上相等,且无协方差,因此形成了一个近似球形的分布。
1.1.5 与渲染参数结合
3DGS的均值与方差与渲染参数是密切相关的,它们决定了每个3D高斯的形状、大小、方向和亮度。
具体来说,3D 高斯的均值 $\mu_i$ 表示了其在空间中的位置,它可以从 SfM 点云中初始化,也可以通过优化算法进行调整,以适应给定的图像序列和视角。3D 高斯的协方差矩阵 $\Sigma_i$ 表示了其在空间中的形状和方向,它可以用一个对称正定矩阵来表示,也可以用一个对角矩阵和一个旋转矩阵的乘积来表示,以减少参数的数量。3D 高斯的协方差矩阵也可以通过优化算法进行调整,以达到最佳的渲染效果。3D 高斯的权重 $w_i$ 表示了其在场景中的贡献,它可以用一个非负的标量来表示,也可以用一个球谐函数来表示,以增加其与视图相关的表达能力。3D高斯的权重也可以通过优化算法进行调整,以保持能量守恒和避免过拟合。
1.2 球谐函数
请参考 球谐函数介绍(Spherical Harmonics)、球谐函数可视化 | 直观理解球谐展开,我个人觉得自己无法比这些文章写得更好了。
1.3 投影变换
上文讨论的分布函数先在模型空间原点用 $\Sigma$ 确定形状与旋转,之后用 $\mu$ 平移到世界空间。为了渲染到画布上需要先 view 变换到相机空间,再 project 变换将透视空间变得和像素对齐才能进行光栅化。如下图,上:相机空间,下:project后的光线空间。
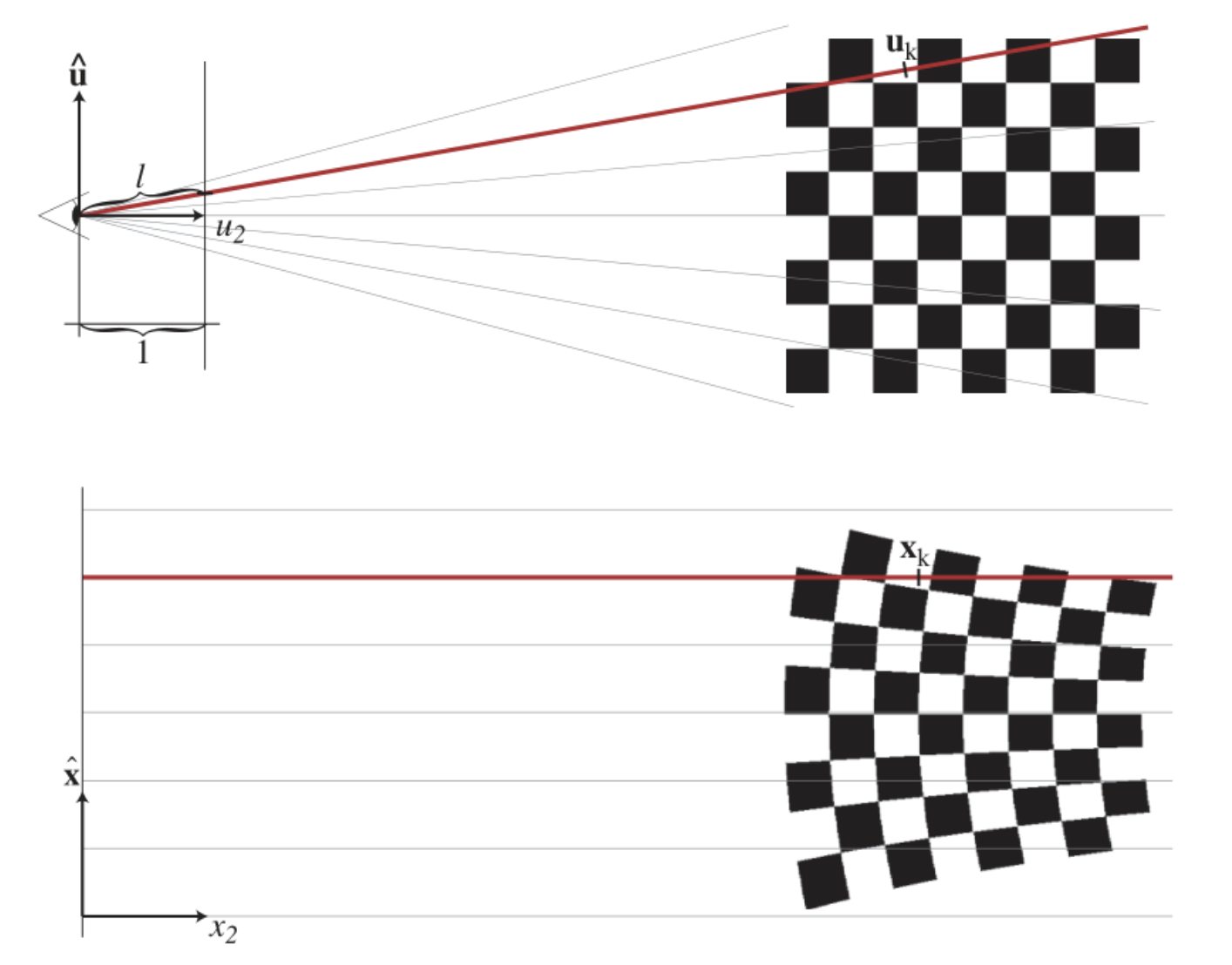
根据论文引用的核心文章 EWA volume splatting(Zwicker et al. [2001a]),取一个点对project矩阵二阶泰勒展开即可得到仿射近似local affine approximation,更具体来说其中雅克比矩阵是project矩阵在这一点对相机空间点的偏导。最后得到的投影如下图:
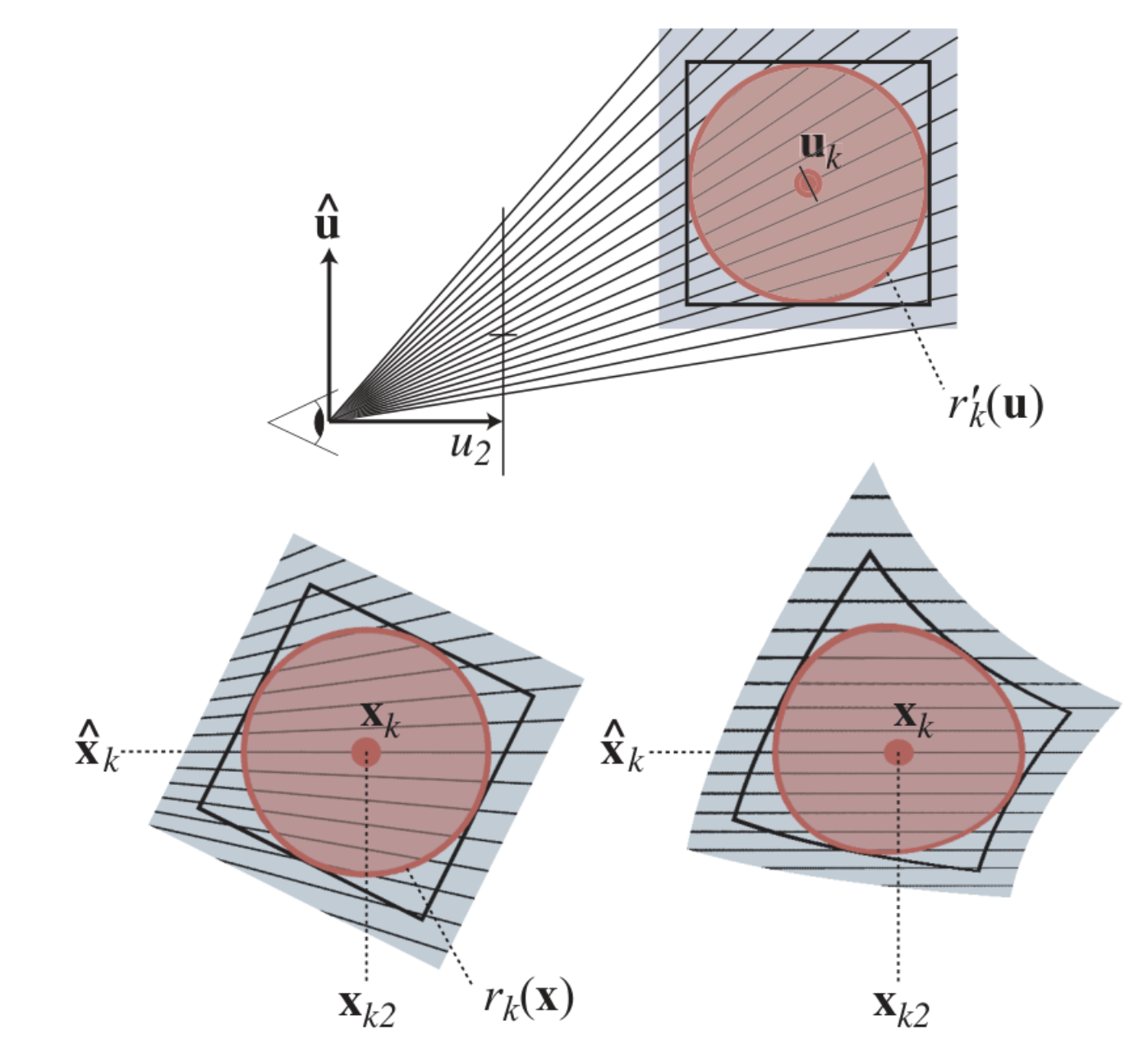
左下是文中得到的近似结果,右下是理想的 project 结果。这样最终变换完的的基础单元仍然是一个 3D 高斯,而且 3D 的前两维对应画布的 2D 像素坐标 $(x,y)$,第三维则对应从像素进入的深度。
2. 代码文件速览
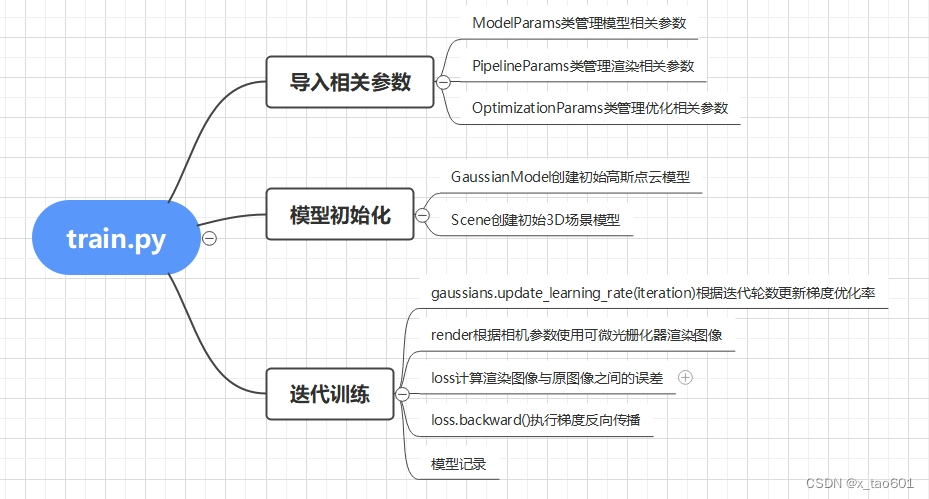
这段代码是用于 3D 重建的 Python 类 GaussianModel。以下是对其关键组成部分的逐步解释:
GaussianModel 类
初始化方法 __init__
- 初始化各种参数,如球谐函数的阶数、位置、特征、缩放、旋转和不透明度。
setup_functions: 配置各种数学和物理模型函数。
方法 setup_functions
- 定义了处理缩放、旋转和不透明度的激活函数。
方法 capture 和 restore
capture: 捕获模型的当前状态。restore: 恢复模型到之前的状态。
属性访问器
get_scaling,get_rotation等:提供对内部参数的访问。
方法 get_covariance
- 生成并返回协方差矩阵,基于缩放和旋转参数。
方法 create_from_pcd
- 从点云数据创建模型。
方法 training_setup
- 设置用于训练的优化器和学习率调度。
方法 update_learning_rate
- 根据迭代次数更新学习率。
方法 save_ply 和 load_ply
- 保存和加载点云数据为 PLY 文件格式。
方法 reset_opacity, replace_tensor_to_optimizer, _prune_optimizer
- 处理不透明度和优化器的参数更新。
方法 prune_points, cat_tensors_to_optimizer, densification_postfix
- 对点云进行剪枝、添加和修改,以改进模型表示。
方法 densify_and_split, densify_and_clone, densify_and_prune
- 增密点云并进行分割和克隆,以优化3D结构。
方法 add_densification_stats
- 收集增密过程中的统计数据。
参考文章
3D Gaussian Splatting for Real-Time Radiance Field Rendering
[NeRF坑浮沉记]3D Gaussian Splatting入门:如何表达几何
A Survey on 3D Gaussian Splatting
3D Gaussian Splatting 渲染过程_gaussian splatting光线空间
论文笔记《3D Gaussian Splatting for Real-Time Radiance Field Rendering》
3D Gaussian Splatting 解读